Derivation of continuity equation in cartesian coordinates

In this article, we are going to derive the continuity equation in three-dimensional cartesian coordinates. Due to some constraints, I have uploaded images of every equation. Fluid elements in the three-dimensional flow diagram are shown below:

Derivation of continuity equation:

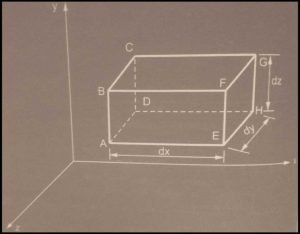
Consider a fluid element control volume with sides dx, dy, and dz as shown in the above figure of a fluid element in three-dimensional flow.

Now let ρ = Mass density of fluid at a particular instant.

u, v, w = Components of the velocity of flow entering three faces of a parallelopiped.

Rate of the mass of fluid entering the face ABCD which is a fluid influx,

= ρ x Velocity in X- direction x (Area of ABCD)

= ρ u dy dz    ………………..eq (1)

Now, Rate of the mass of fluid leaving the face EFGH (fluid efflux),

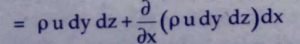
The gain in mass per unit time due to flow in X- direction is given by the difference between the fluid influx and fluid efflux.

Therefore, mas accumulated per unit time due to flow in X- direction,

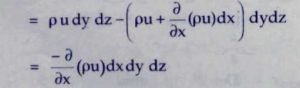
Similarly the gain in fluid mass per unit time in the parallelopiped due to flow in Y and Z directions,

The net gain in fluid mass per unit for fluid along three co-ordinate axes,

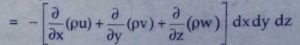
The rate of change of mass of the parallelopiped (control volume) is,

From equating eq(6) and eq(7), we get,

Read More Working of thermosyphon cooling system in IC engine

Final Continuity Equation:

Now simplify the above equation and rearrange the terms to get continuity equation in cartesian coordinates,

therefore,

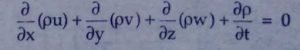
The above equation is the general equation of continuity in three dimensions. This continuity equation is applicable for compressible flow as well as an incompressible flow.

Our Downloads:

Download continuity equation derivation pdf from => GDrive

In this way, we have seen the derivation of continuity equation in 3D cartesian coordinates. Feel free to discuss your queries in the comment section.