Euler’s and Bernoulli’ equation : Derivation, Assumptions, Limitations

In this article, we are going to get derive Euler’s equation of motion along a streamline and from that, we will derive Bernoulli’s equation. So, let’s dive into it.

Derivation of Euler’s equation:

Consider streamflow of incompressible non-viscous fluid and the cylindrical element of fluid with cross-sectional area δA and length δS moving along streamline as shown in the above figure.

Read More:  Derivation of continuity equation in cartesian coordinates

Let V be the velocity and “as” be the acceleration,

Pressure force on lower face = p.δA

Pressure force on upper face =

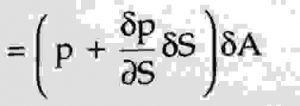
Now,

Net pressure force is,

Weight of element γδAδS is acting through the center of gravity in a vertically downward direction.

Fgs =  γδAδS cosθ

Now,

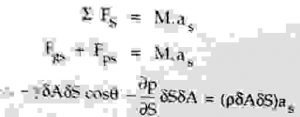
divide the above equation by δAδS,

we get,

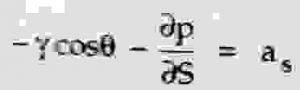
Now, V is a function of s and t , V = f (s, t)

Divide the above equation by ρ and we get

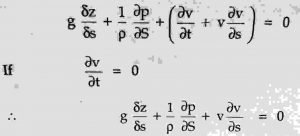
Further, we get,

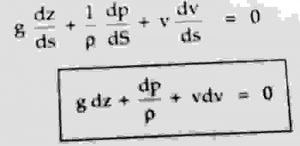
This is the final Euler’s equation of motion.

Let a small cylindrical fluid element in a stream tube be having a cross-sectional area ‘dA’ such that its weight ‘W’ makes an angle of θ with the axis of the element.

Let the length of the element be ‘ds’ and pressure at upstream and downstream faces be P and (p + dp/ds . ds) respectively.

From certain datum, let elevation difference between circular faces of the element be ‘dz’.

Hence we have cos θ = dz/ds.

For steady flow, acceleration of fluid is given as,

Also, the mass and weight of fluid elements are given as ρdAds and ρgdAds respectively.

Assumptions of Euler’s Equation:

1. Only pressure and gravity forces are dominant and all other forces are negligible
2. Flow is steady
3. The fluid is ideal and non-viscous

Apply Newton’s second law of motion to the above equation,

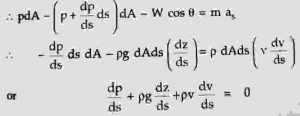
Above equation can also be written as,

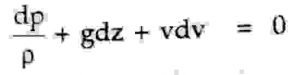
The above equation is known as Euler’s equation.

Derivation of Bernoulli’s equation:

Now let’s get a derivation of Bernoulli’s equation from Euler’s equation.

For an incompressible fluid, ρ is constant.

Hence the integration of Euler’s equation gives,

This is the required form of Bernoulli’s equation or energy equation, where each term represents the energy head means energy per unit weight of the fluid.

Assumptions of Bernoulli’s Equation:

Following assumptions are made in the derivation of Bernoulli’s equation:

1. The fluid is incompressible
2. The flow is steady and continuous.
3. The fluid is non-viscous
4. The flow is irrotational
5. The gravity and pressure forces are only considered
6. The equation is applicable along a stram line only
7. The velocity is uniform over the cross-section

Read More: Working of thermosyphon cooling system in IC engine

Limitations of Bernoulli’s Equation:

1. The fluid is not ideal. Hence, due to no sleep condition, the velocity at the fixed boundary is zero and it does not increase.
2. Its means, the velocity across the section is not uniform,
3. Practically, in addition to gravity and pressure forces, some forces like the viscous force is also involved in the motion of the fluid.
4. When the fluid passes from one section to another, some energy addition or subtraction takes place.

Conclusion:

In this brief article, we have derived the Euler’s equation of motion and made its assumptions. We have also explained the derivation of Bernoulli’s equation and it’s limitations, also, made its assumptions. If you have any queries regarding this article, feel free to use our comment section.